五角形の比

Q

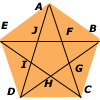
正五角形の全ての対角線を結ぶと図に示すように真中に小さな正五角形ができます。もとの正五角形との辺の長さの比はどれくらいでしょう？

A

きれいな数値になるかと思いましたが、期待はずれでした。でも、値を求める過程はなかなかエレガントです。以下簡単のために、大きな正五角形の一辺の長さを1とし、小さな正五角形の一辺の長さを

x とします。

まずは、三角形の相似に着目です。△HEBと△HCDは相似なので、EB:DC=EH:CHという比例関係が成り立ちます。ここで、DCは1です。また、四角形BAEHは平行四辺形なので、EHが1、CHが1-x、EBが2-xになります。すると、この比例式は、(2-x):1=1:(1-x)と書け、内項と外項同士をかけあわせて、(2-x)(1-x)=1。展開して移項するとx²-3x+1=0という二次方程式になります。

あとは解の公式で、x=(3±√5)/2となりますが、プラスの方だと値が1以上になっておかしいので、マイナスの方のx=(3-√5）/2が正解です。だいたい、0.382くらいです。